Redis——BitMap
1 基本命令
Redis提供了SETBIT、GETBIT、BITCOUNT、BITOP四个常用命令用于处理二进制位数组。
SETBIT:为位数组指定偏移量上的二进制位设置值,偏移量从0开始计数,二进制位的值只能为0或1。返回原位置值。GETBIT:获取指定偏移量上二进制位的值。BITCOUNT:统计位数组中值为1的二进制位数量。BITOP:对多个位数组进行按位与、或、异或运算。
2 源码分析
2.1 数据结构
扩展:Redis 中的每个对象都是有一个 redisObject 结构表示的。
typedef struct redisObject { // 类型 unsigned type:4; // 编码 unsigned encoding:4; unsigned lru:REDIS_LRU_BITS; /* lru time (relative to server.lruclock) */ // 引用计数 int refcount; // 执行底层实现的数据结构的指针 void *ptr; } robj;
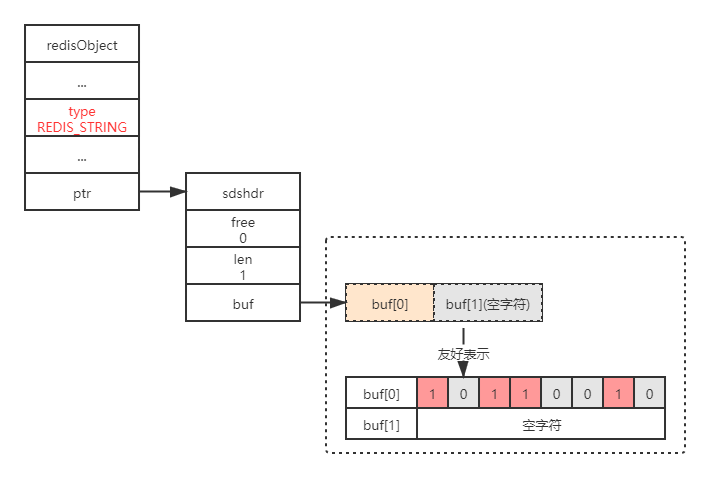
type的值为REDIS_STRING表示这是一个字符串对象sdshdr.len的值为1表示这个SDS保存了一个1字节大小的位数组- buf数组中的
buf[0]实际保存了位数组 - buf数组中的
buf[1]为自动追加的\0字符
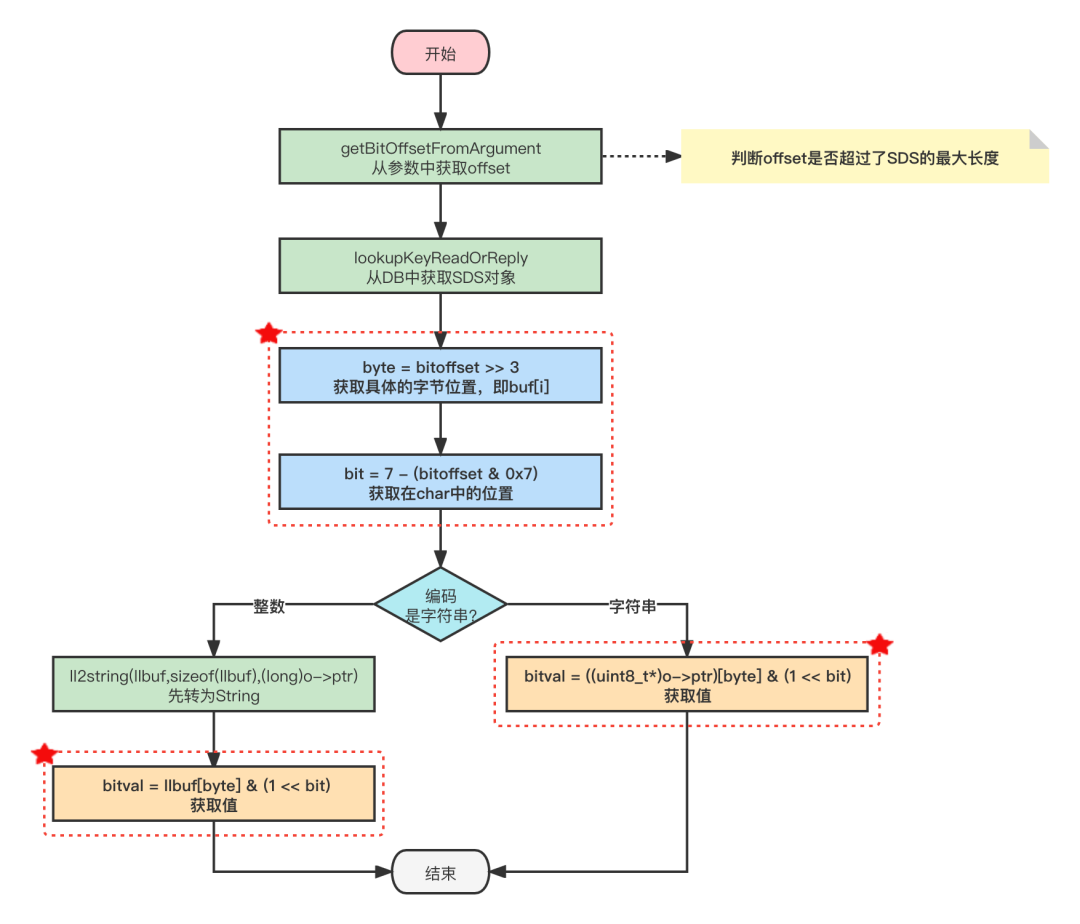
3.2 GETBIT
GETBIT用于返回位数组在偏移量上的二进制位的值。**GETBIT的时间复杂度是O(1)。**
GETBIT命令的执行过程如下:
- 计算byte=⌊offset÷8⌋ (即
>>3),byte 值表示指定的 offset 位于位数组的哪个字节(计算在第几行); - 指定 buf[i]中的i了,接下来就要计算在8个字节中的第几位:使用
bit=(offset % 8)+1(取模运算用位运算取最低三位代替)计算可得; - 根据 byte 和 bit在位数组中定位到目标值返回即可。
源码:
void getbitCommand(client *c) {
robj *o;
char llbuf[32];
uint64_t bitoffset;
size_t byte, bit;
size_t bitval = 0;
// 获取offset
if (getBitOffsetFromArgument(c,c->argv[2],&bitoffset,0,0) != C_OK)
return;
// 查找对应的位图对象
if ((o = lookupKeyReadOrReply(c,c->argv[1],shared.czero)) == NULL ||
checkType(c,o,OBJ_STRING)) return;
// 计算offset位于位数组的哪一行
byte = bitoffset >> 3;
// 计算offset在一行中的第几位,等同于取模,取最后几位
bit = 7 - (bitoffset & 0x7);
// #define sdsEncodedObject(objptr) (objptr->encoding == OBJ_ENCODING_RAW || objptr->encoding == OBJ_ENCODING_EMBSTR)
if (sdsEncodedObject(o)) {
// SDS 是RAW 或者 EMBSTR类型
if (byte < sdslen(o->ptr))
// 获取指定位置的值
// 注意它不是真正的一个二维数组不能用((uint8_t*)o->ptr)[byte][bit]去获取呀~
bitval = ((uint8_t*)o->ptr)[byte] & (1 << bit);
} else {
// SDS 是 REDIS_ENCODING_INT 类型的整数,先转为String
if (byte < (size_t)ll2string(llbuf,sizeof(llbuf),(long)o->ptr))
bitval = llbuf[byte] & (1 << bit);
}
addReply(c, bitval ? shared.cone : shared.czero);
}
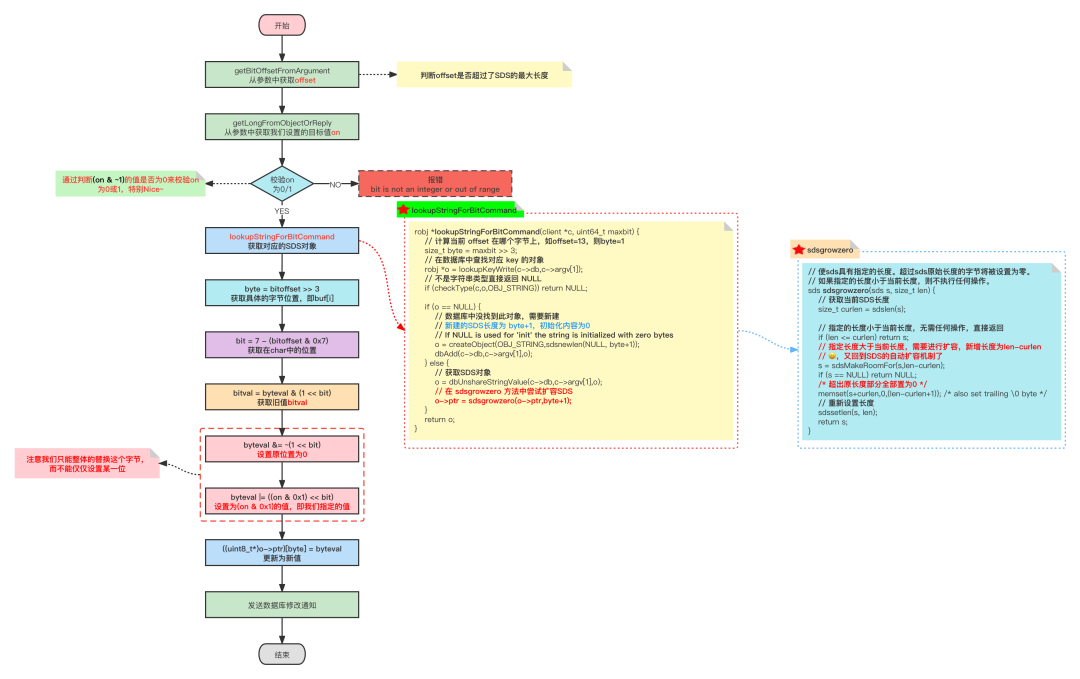
3.3 SETBIT
SETBIT用于将位数组在偏移量的二进制位的值设为value,并向客户端返回旧值。
SITBIT命令的执行过程如下:
- 计算len=⌊offset÷8⌋+1,len值记录了保存offset偏移量指定的二进制位至少需要多少字节
- 检查位数组的长度是否小于len,如果是的话,将SDS的长度扩展为len字节,并将所有新扩展空间的二进制位设置为0
- 计算byte=⌊offset÷8⌋,byte值表示指定的offset位于位数组的那个字节(就是计算在那个buf[i]中的iii)
- 使用bit=(offset mod 8)+1计算可得目标buf[i]的具体第几位
- 根据byte和bit的值,首先保存oldValue,然后将新值value设置到目标位上
- 返回旧值
因为SETBIT命令执行的所有操作都可以在常数时间内完成,所以该命令的算法复杂度为O(1)。
SETBIT命令源码如下所示:
void setbitCommand(client *c) {
robj *o;
char *err = "bit is not an integer or out of range";
uint64_t bitoffset;
ssize_t byte, bit;
int byteval, bitval;
long on;
// 获取offset
if (getBitOffsetFromArgument(c,c->argv[2],&bitoffset,0,0) != C_OK)
return;
// 获取我们需要设置的值
if (getLongFromObjectOrReply(c,c->argv[3],&on,err) != C_OK)
return;
/* 判断指定值是否为0或1 */
if (on & ~1) {
// 设置了0和1之外的值,直接报错
addReplyError(c,err);
return;
}
// 根据key查询SDS对象(会自动扩容)
if ((o = lookupStringForBitCommand(c,bitoffset)) == NULL) return;
/* 获得当前值 */
byte = bitoffset >> 3;
byteval = ((uint8_t*)o->ptr)[byte];
bit = 7 - (bitoffset & 0x7);
bitval = byteval & (1 << bit);
/* 更新值并返回旧值 */
byteval &= ~(1 << bit);
byteval |= ((on & 0x1) << bit);
((uint8_t*)o->ptr)[byte] = byteval;
// 发送数据修改通知
signalModifiedKey(c,c->db,c->argv[1]);
notifyKeyspaceEvent(NOTIFY_STRING,"setbit",c->argv[1],c->db->id);
server.dirty++;
addReply(c, bitval ? shared.cone : shared.czero);
}(这个图我真的,我哭鼠,他是真的想让我学会的😭)
2.4 BITCOUNT
BITCOUNT命令用于统计给定位数组中值为1的二进制位的数量。功能似乎不复杂,但实际上要高效地实现这个命令并不容易,需要用到一些精巧的算法。
统计一个位数组中非0二进制位的数量在数学上被称为”计算汉明重量”。
二进制位统计算法:variable-precision SWAR
目前已知效率最好的通用算法为variable-precision SWAR算法,该算法通过一系列位移和位运算操作,可以在常数时间内计算多个字节的汉明重量,并且不需要使用任何额外的内存
算法代码:
uint32_t swar(uint32_t i) {
// 5的二进制:0101
i = (i & 0x55555555) + ((i >> 1) & 0x55555555);
// 3的二进制:0011
i = (i & 0x33333333) + ((i >> 2) & 0x33333333);
i = (i & 0x0F0F0F0F) + ((i >> 4) & 0x0F0F0F0F);
i = (i*(0x01010101) >> 24);
return i;
//——————————上面为展开版,下面为更简洁版——————————————
i = i - ((i >> 1) & 0x55555555);
i = (i & 0x33333333) + ((i >> 2) & 0x33333333);
return (((i + (i >> 4)) & 0x0F0F0F0F) * 0x01010101) >> 24;
}- 步骤一计算出的值i的二进制表示可以按每两个二进制位为一组进行分组,各组的十进制表示就是该组的1的数量;
- 步骤二计算出的值i的二进制表示可以按每四个二进制位为一组进行分组,各组的十进制表示就是该组的1的数量;
- 步骤三计算出的值i的二进制表示可以按每八个二进制位为一组进行分组,各组的十进制表示就是该组的1的数量;
- 步骤四的
i*0x01010101语句计算出bitarray中1的数量并记录在二进制位的最高八位,而>>24语句则通过右移运算,将bitarray的汉明重量移动到最低八位,得出的结果就是bitarray的汉明重量。
Integer.bitCount方法,也是基于SWAR算法的思想
2.4.4 源码分析
Redis 中通过调用redisPopcount方法统计汉明重量,源码如下所示:
long long redisPopcount(void *s, long count) {
long long bits = 0;
unsigned char *p = s;
uint32_t *p4;
// 为查表法准备的表
static const unsigned char bitsinbyte[256] = {0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,1,2,2,3,2,3,3,4,2,3,3,4,3,4,4,5,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,2,3,3,4,3,4,4,5,3,4,4,5,4,5,5,6,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,3,4,4,5,4,5,5,6,4,5,5,6,5,6,6,7,4,5,5,6,5,6,6,7,5,6,6,7,6,7,7,8};
// CPU一次性读取8个字节,如果4字节跨了两个8字节,需要读取两次才行
// 所以考虑4字节对齐,只需读取一次就可以读取完毕
while((unsigned long)p & 3 && count) {
bits += bitsinbyte[*p++];
count--;
}
// 一次性处理28字节,单独看一个aux就容易理解了,其实就是SWAR算法
// uint32_t:4字节
p4 = (uint32_t*)p;
while(count>=28) {
uint32_t aux1, aux2, aux3, aux4, aux5, aux6, aux7;
aux1 = *p4++;// 一次性读取4字节
aux2 = *p4++;
aux3 = *p4++;
aux4 = *p4++;
aux5 = *p4++;
aux6 = *p4++;
aux7 = *p4++;
count -= 28;// 共处理了4*7=28个字节,所以count需要减去28
aux1 = aux1 - ((aux1 >> 1) & 0x55555555);
aux1 = (aux1 & 0x33333333) + ((aux1 >> 2) & 0x33333333);
aux2 = aux2 - ((aux2 >> 1) & 0x55555555);
aux2 = (aux2 & 0x33333333) + ((aux2 >> 2) & 0x33333333);
aux3 = aux3 - ((aux3 >> 1) & 0x55555555);
aux3 = (aux3 & 0x33333333) + ((aux3 >> 2) & 0x33333333);
aux4 = aux4 - ((aux4 >> 1) & 0x55555555);
aux4 = (aux4 & 0x33333333) + ((aux4 >> 2) & 0x33333333);
aux5 = aux5 - ((aux5 >> 1) & 0x55555555);
aux5 = (aux5 & 0x33333333) + ((aux5 >> 2) & 0x33333333);
aux6 = aux6 - ((aux6 >> 1) & 0x55555555);
aux6 = (aux6 & 0x33333333) + ((aux6 >> 2) & 0x33333333);
aux7 = aux7 - ((aux7 >> 1) & 0x55555555);
aux7 = (aux7 & 0x33333333) + ((aux7 >> 2) & 0x33333333);
bits += ((((aux1 + (aux1 >> 4)) & 0x0F0F0F0F) +
((aux2 + (aux2 >> 4)) & 0x0F0F0F0F) +
((aux3 + (aux3 >> 4)) & 0x0F0F0F0F) +
((aux4 + (aux4 >> 4)) & 0x0F0F0F0F) +
((aux5 + (aux5 >> 4)) & 0x0F0F0F0F) +
((aux6 + (aux6 >> 4)) & 0x0F0F0F0F) +
((aux7 + (aux7 >> 4)) & 0x0F0F0F0F))* 0x01010101) >> 24;
}
/* 剩余的不足28字节,使用查表法统计 */
p = (unsigned char*)p4;
while(count--) bits += bitsinbyte[*p++];
return bits;
}Redis 中同时运用了查表法和SWAR算法完成BITCOUNT功能。
3 应用
大量数据去重、排序、用户签到、统计活跃用户、实现布隆过滤器,下面详细介绍布隆过滤器
布隆过滤器简介和算法流程
主要特征
一种紧凑型的、比较巧妙的概率型数据结构,它由一个很长的二进制向量( 位向量)和一系列随机均匀分布的散列( 哈希)函数组成 此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
存在假阳性(将不在集合中的元素误判为在集合中),不存在假阴性(将在集合中的元素误判为不在集合中)。过滤器中的元素个数越多,假阳性的可能性越大,总的来说,当不考虑集合中元素个数的情况下,每个元素由10个以下的bit来表示就可以保证1%以内的假阳性概率。
元素可以被加入过滤器,但不可从过滤器中删除(因为删除的时候有可能会影响到其他元素,之后会细说)。
空间和时间优势
布隆过滤器不需要存储数据项,但是同时它需要在其他地方单独存储真正的数据项。对于一个拥有最优k值且误判率在1%的布隆过滤器,每个元素只需要9.6bits(与元素的大小无关)。这个优点一部分继承自数组的紧凑性,另一方面由它本身的概率性决定。若给每个元素增加4.8bits左右,误判率将会减少十倍。
布隆过滤器在添加和查找元素时,所需要的时间是一个常数,O(k),完全与集合中元素个数无关。没有其他固定空间的集合数据结构有这样的效率,但是对于稀疏散列表来说,平均访问时长在实际使用中比一些布隆过滤器要短。在硬件实现方式中,布隆过滤器的优势在于他的k个查询之间不相关,因此可以并行处理。
布隆过滤器(Bloom Filter)的核心实现是一个超大的位数组和几个哈希函数。假设位数组的长度为m,哈希函数的个数为k
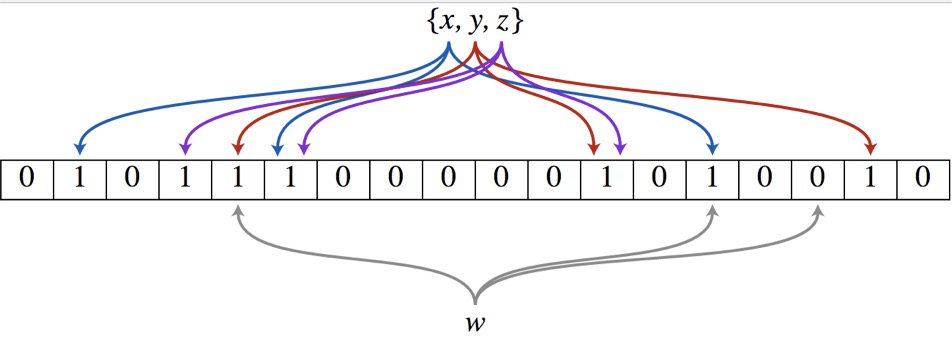
以上图为例,具体的操作流程:
假设集合里面有3个元素{x, y, z},哈希函数的个数为3。
首先将位数组进行初始化,将里面每个位都设置位0。
对于集合里面的每一个元素,将元素依次通过3个哈希函数进行映射,每次映射都会产生一个哈希值,这个值对应位数组上面的一个点,然后将位数组对应的位置标记为1。
查询W元素是否存在集合中的时候,同样的方法将W通过哈希映射到位数组上的3个点。
如果3个点的其中有一个点不为1,则可以判断该元素一定不存在集合中。
反之,如果3个点都为1,则该元素可能存在集合中。
注意:此处不能判断该元素是否一定存在集合中,可能存在一定的误判率。可以从图中可以看到:假设某个元素通过映射对应下标为4,5,6这3个点。虽然这3个点都为1,但是很明显这3个点是不同元素经过哈希得到的位置,因此这种情况说明元素虽然不在集合中,也可能对应的都是1,这是误判率存在的原因。
Redis实现
谷歌公司提供的Guava 工具提供了布隆过滤器的实现,先不分析源码了吧,有机会补上【【flag】】
布隆过滤器应用(反正过滤就对了)
- 字处理软件中,需要检查一个英语单词是否拼写正确
- 在 FBI,一个嫌疑人的名字是否已经在嫌疑名单上
- 在网络爬虫里,一个网址是否被访问过
- yahoo, gmail等邮箱垃圾邮件过滤功能
联想一下:分布式数据库TiDB的TiKV使用的底层RocksDB查询就利用了bloom filter不存在假阴性加快查找速度。
(布隆过滤器的内容也来源网络,看了好几个都大差不差,所以就省略哩)
.png)